Classical dynamical localization
Bridging classical chaos and quantum localization phenomena.
This work explores classical models of the kicked rotor, where momentum updates are constrained to multiples of a constant step size. Despite being purely classical, these systems exhibit striking analogies to quantum phenomena such as dynamical localization and quantum resonances.
The dynamics are governed by a generalized map on the torus:
\[p_{t+1} = p_t + V'(\theta_t), \quad \theta_{t+1} = \theta_t + p_{t+1}\]with a piecewise-linear periodic potential \(V(\theta)\) whose slope takes only discrete values:
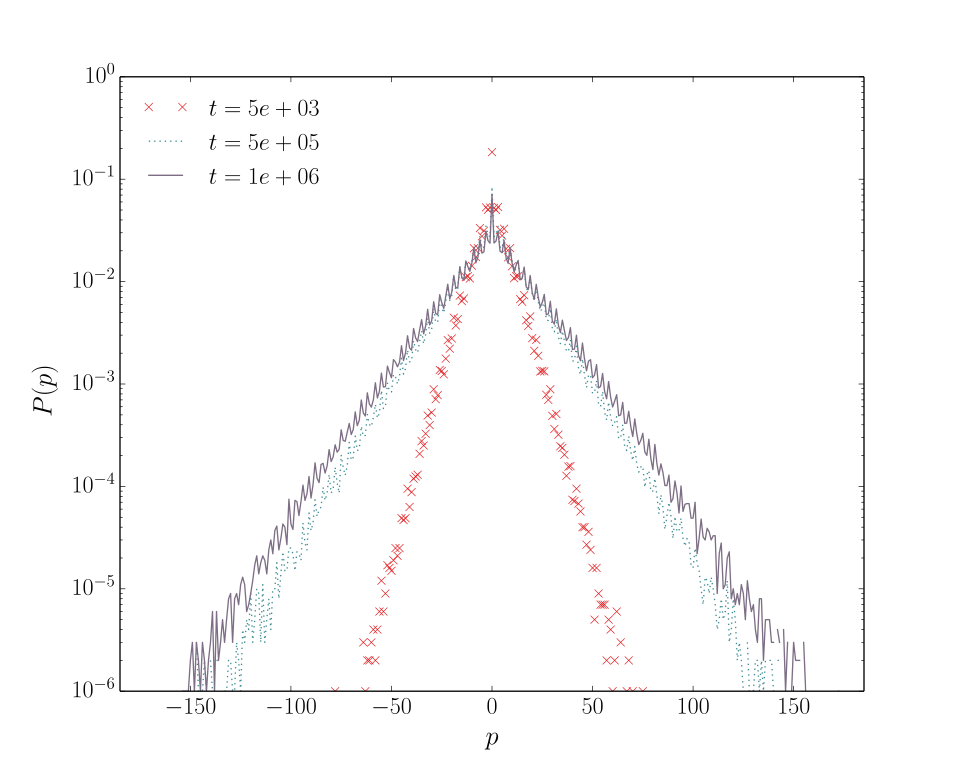
\[V'(\theta) \in \{ j \, \eta \mid j \in \mathbb{Z} \}, \quad \eta > 0.\]For irrational values of \(\eta / (2\pi)\), momentum growth is suppressed, leading to quasi-localization characterized by slow, logarithmic spreading. Momentum distributions then take on exponential profiles reminiscent of quantum localization.
In contrast, when \(\eta / (2\pi)\) is rational, ballistic transport occurs with quadratic energy growth:
\[\langle p^2(t) \rangle \sim t^2,\]closely mirroring the quantum resonances of the kicked rotor.
These results demonstrate that features often regarded as purely quantum — localization and resonances — can emerge in classical dynamics due to conservation laws and phase-space discreteness, prompting a reevaluation of the boundary between classical chaos and quantum coherence.