Area-Law Entangled Eigenstates from Nullspaces of Local Hamiltonians
Generating area-law entangled eigenstates via nullspace engineering.
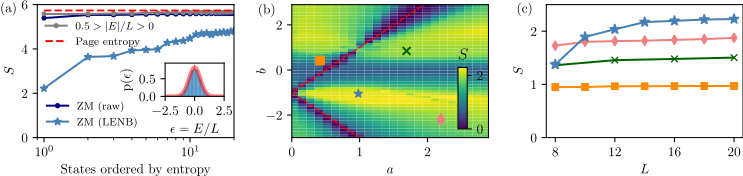
This paper investigates how nullspaces of local Hamiltonians provide a general route to constructing non-thermal eigenstates that violate the eigenstate thermalization hypothesis (ETH). While ETH predicts that highly excited eigenstates resemble random vectors with volume-law entanglement, we show that certain zero-energy modes (zero modes) within the nullspace instead obey an area-law scaling of entanglement entropy, making them analogues of quantum many-body scars.
We focus on spin-$1/2$ chains with inversion and spectral reflection symmetry, described by the Hamiltonian
\(H_{ZXZ} = \sum_{i=1}^{L} \Big[ X_i + a \,(Z_i X_{i+1} + X_i Z_{i+1}) + b \, Z_{i-1} X_i Z_{i+1} \Big],\)
where $X_i, Z_i$ are Pauli matrices acting on site $i$, and parameters $a, b$ tune two-body and three-body interactions. Due to the anticommutation relation ${H_{ZXZ}, \Pi} = 0$ with $\Pi = \prod_i Z_i$, the spectrum is symmetric around zero energy, guaranteeing an exponentially large nullspace with
\(D_0 = \dim(\ker H_{ZXZ}) \geq 2^{L/2}.\)
To systematically explore the nullspace, we introduce the least entangled nullspace basis (LENB), constructed by iteratively minimizing the bipartite entanglement entropy
\(S = -\mathrm{Tr}\, \rho_A \ln \rho_A,\)
where $\rho_A$ is the reduced density matrix of half the chain. The first state in this ordering, the least entangled zero mode (LEZM), exhibits area-law scaling even for generic parameters,
\(S(L) \sim \mathcal{O}(1),\)
contrasting with the volume-law $S(L) \sim L$ of typical eigenstates. Numerical results confirm this across broad regions of parameter space.
We further study kinetically constrained models, such as the range-2 PXP Hamiltonian,
\(H_{PPXP} = \sum_i P_{i-2} P_{i-1} X_i P_{i+1} P_{i+2},\)
with projectors $P_i = (1 - Z_i)/2$. Here, we identify analytically a simple product of two-site singlets and dimers that forms an exact LEZM. Using simulations of realistic Rydberg atom arrays, we show that such zero modes can be prepared and remain robust against perturbations over experimentally relevant timescales.
Our results establish a generic mechanism for weak ergodicity breaking: any local Hamiltonian with an exponentially large nullspace hosts at least one area-law entangled eigenstate. This provides a new perspective on quantum many-body scars, suggests efficient MPS-based algorithms for constructing such states, and opens experimental opportunities in Rydberg atom systems.