Topological charges of periodically kicked molecules
Topological charges and protection in periodically driven molecular systems.
This work explores how even the simplest molecules—closed-shell diatomics—can exhibit nontrivial topological behavior when driven by periodic, far-off-resonant laser pulses. A linear molecular rotor subject to periodic kicks can be mapped onto a crystalline lattice in angular momentum space, which enables the definition of quasimomenta and Floquet band structures, closely resembling Bloch waves in solids.
The molecular Hamiltonian under short pulses takes the form
\(\hat{H}_{\text{mol}}(t) = B\hat{L}^2 - \big[P_1 \cos^2(\hat{\theta}) + P_2 \cos(\hat{\theta}) \big]\sum_{q=0}^{\infty}\delta(t - qT),\)
where $B$ is the rotational constant, $\hat{L}$ the angular momentum operator, and $P_1, P_2$ characterize the pulse strengths. After one driving period, the evolution is described by the Floquet operator
\(\hat{U} = e^{-\pi i \hat{L}^2/N} e^{i \hat{V}(P_1,P_2)},\)
with $T = \tau_B/N$ corresponding to quantum resonance.
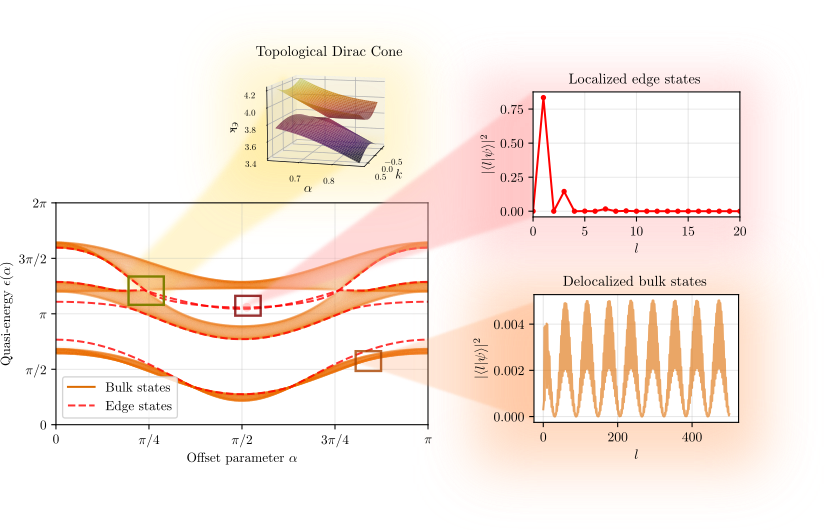
By mapping the system into quasimomentum space, the periodically driven molecule admits a tight-binding description, allowing the construction of “molecular Bloch bands.” For the case $N=3$, the effective band structure shows Dirac cones that are topologically protected by reflection and time-reversal symmetry. Choosing a parametrization of the pulse strengths,
\(P_1(\alpha) = P \cos^2(\alpha), \quad P_2(\alpha) = P \sin^2(\alpha),\)
one finds that the quasienergies $\epsilon_n(k,\alpha)$ host Dirac points at $k=\pi$. The associated Berry phase around these points evaluates to $\pm \pi$, confirming their role as topological charges.
The consequences are directly observable in experiments: as a molecule is adiabatically driven through such Dirac cones, its orientation $\langle \cos(\hat{\theta}) \rangle$ and alignment $\langle \cos^2(\hat{\theta}) \rangle$ undergo distinct flips, as shown in time-evolution simulations. These signatures can be measured via standard rotational spectroscopy techniques.
This approach paves the way toward engineering topologically protected states in molecular systems, bridging rotational dynamics with condensed matter concepts such as Dirac cones, edge states, and symmetry-protected phases.