Anomalous multi-gap topological phases in periodically driven quantum rotors

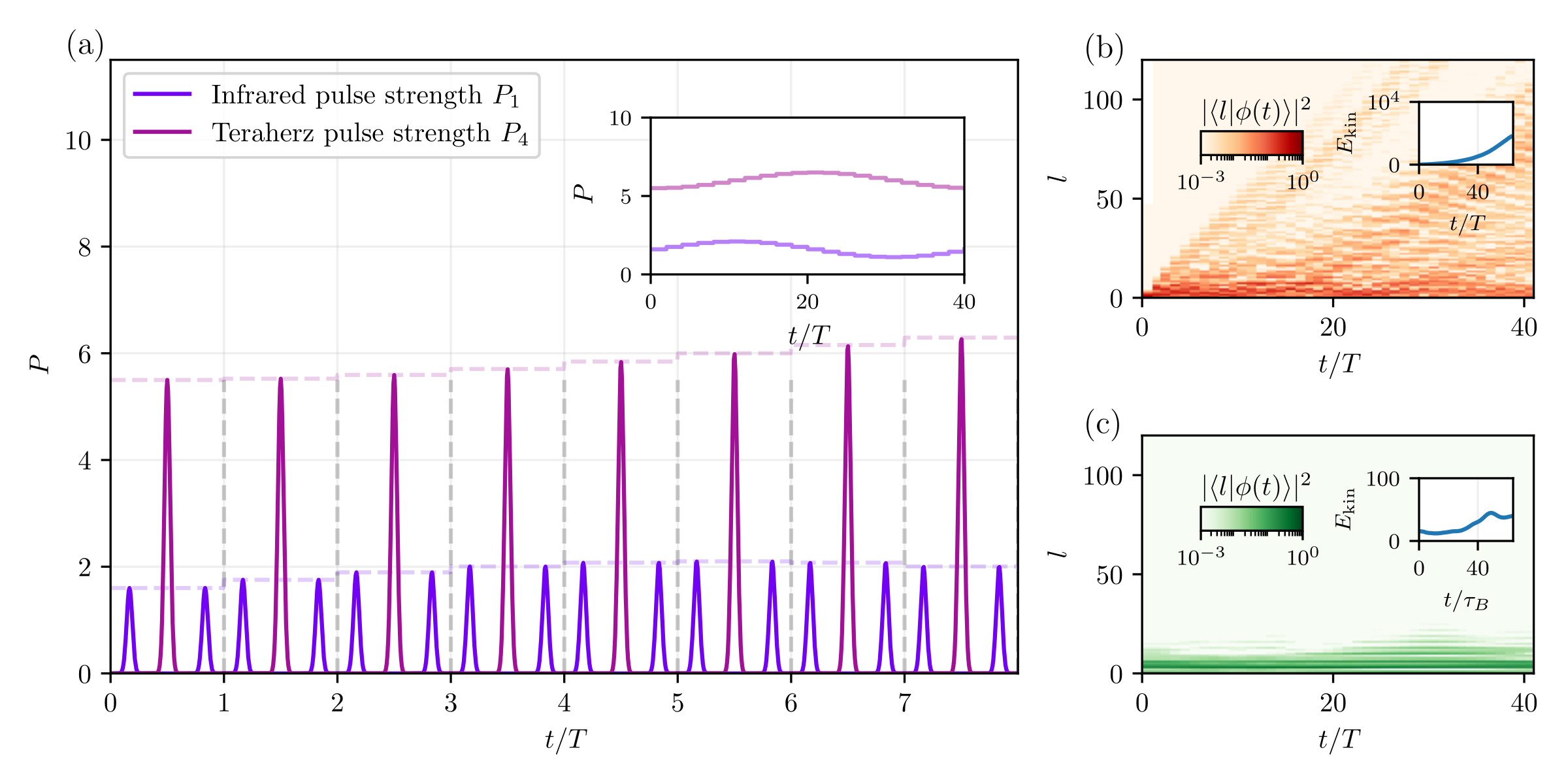
In this project, we show that periodically driven quantum rotors provide a versatile platform for realizing multi-gap topological phases, i.e. regimes where groups of quasienergy bands acquire non-Abelian topological invariants due to braiding of band degeneracies. Unlike equilibrium systems, this setting allows for the emergence of novel out-of-equilibrium phases, most notably an anomalous Dirac string phase characterized by zero-angular-momentum edge states across all quasienergy gaps.

We consider a three-dimensional quantum rotor periodically driven by ultrashort laser pulses. The free-rotor Hamiltonian is
\(H_0 = \frac{\pi \hat{L}^2}{\tau_B},\)
with rotational period $\tau_B$. A single alignment pulse yields the effective potential
\(\hat{V}(P_1, P_2) = P_1 \cos(\hat{\theta}) + P_2 \cos^2(\hat{\theta}),\)
where $\hat{\theta}$ is the angle between rotor and laser polarization.

The Floquet operator for one kick is
\(U_{\text{KR}}(P_1, P_2) = e^{-i \pi \hat{L}^2 \tau / (2 \tau_B)} \, e^{i \hat{V}(P_1, P_2)} \, e^{-i \pi \hat{L}^2 \tau / (2 \tau_B)},\)
with pulse period $\tau$. At quantum resonance, $\tau = 2\tau_B / N$, the system hosts $N$ quasienergy bands.

The stroboscopic Hamiltonian is defined as
\(H_{\text{KR}} = \frac{i}{\tau} \log U_{\text{KR}},\)
with eigenstates $\psi_n(k)$ and quasienergies $\epsilon_n(k)$. The system obeys both inversion $P$ and time-reversal $T$ symmetries:
\(P H_{\text{KR}}(k) = H_{\text{KR}}(-k) P, \qquad T H_{\text{KR}}(k) = H_{\text{KR}}^*(-k) T.\)

By tuning pulse strengths, we induce nodal lines in the Floquet spectrum. Braiding these nodal lines flips their associated non-Abelian frame charges, captured by the Euler class
\(\chi^D_{n,n+1} = \frac{1}{2\pi} \left( \int_D Eu(k)\, dk \wedge d\alpha - \int_{\partial D} A \cdot dk \right) \in \mathbb{Z}.\)

Our main results show that an anomalous Dirac string phase emerges, where all quasienergy gaps, including the anomalous $\pi$-gap, host nodal lines. This leads to edge states even though equilibrium invariants (Zak phases) vanish. Band nodes acquire quaternion-valued charges ${\pm 1, \pm i, \pm j, \pm k}$, which change sign when braided with nodes in adjacent gaps. Finally, we discuss how these phenomena are directly applicable to experiments with laser-driven linear molecules, quantum nanorotors, and synthetic rotors in optical lattices, making the results experimentally testable.